Supported by Dr. Osamu Ogasawara and  providing providing  . . |
|
Last data update: 2014.03.03 |
Euclidean random variableDescriptionClass of Euclidean random variables. Objects from the ClassObjects can be created by calls of the form Slots
ExtendsClass Methods
Author(s)Matthias Kohl Matthias.Kohl@stamats.de See Also
Examples
L1 <- list(function(x){x}, function(x){x^2}, function(x){x^3}, function(x){x^4})
L2 <- list(function(x){exp(x)}, function(x){abs(x)},
function(x){sin(x)}, function(x){floor(x)})
R1 <- new("EuclRandVariable", Map = L1, Domain = Reals(), Range = Reals())
dimension(R1)
Map(R1)
Range(R1)
R1[2]
Map(R1[3])
Map(R1[c(1,2,4)])
Map(R1[2:4])
set.seed(123)
evalRandVar(R1, rnorm(1))
x <- as.matrix(rnorm(10))
res.R1 <- evalRandVar(R1, x)
res.R1[2,,] # results for Map(R1)[[2]](x)
res.R1[2,1,] # results for Map(R1)[[2]](x[1,])
R2 <- EuclRandVariable(L2, Domain = Reals(), dimension = 1)
dimension(R2)
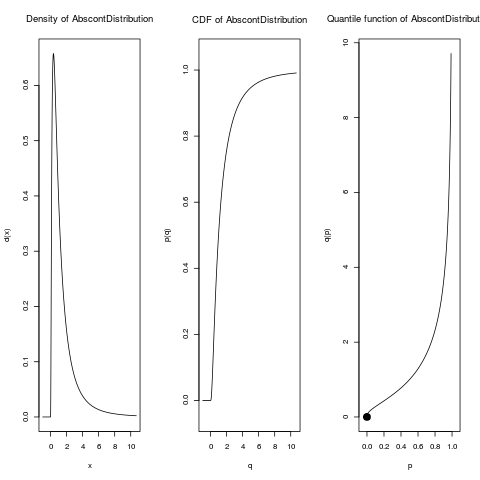
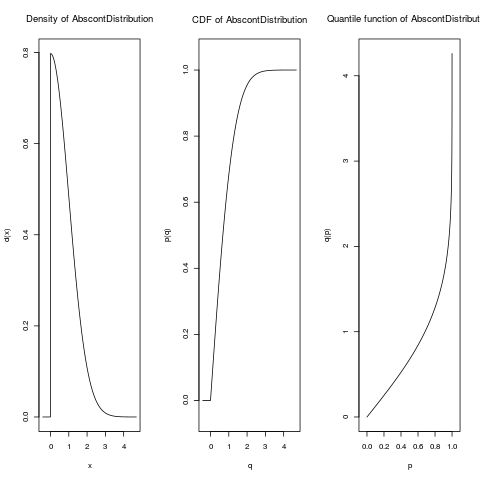
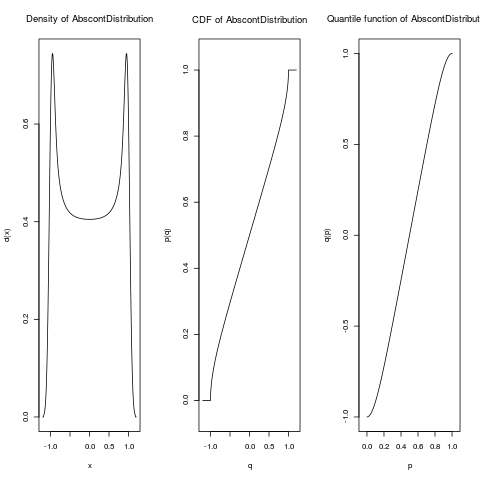
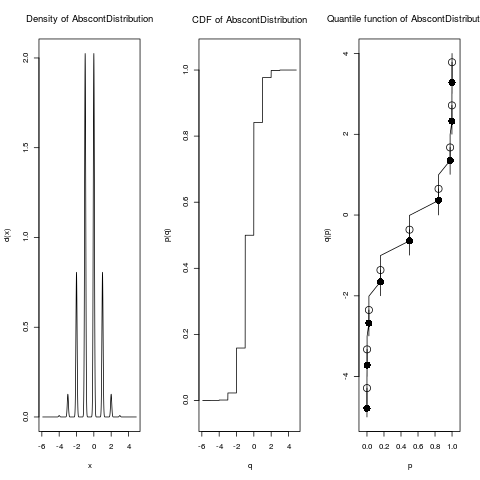
DL1 <- imageDistr(R2, Norm())
plot(DL1)
Domain(R2) <- EuclideanSpace(dimension = 2)
Range(R2) <- EuclideanSpace(dimension = 2)
dimension(R2)
(X <- matrix(c(x, rnorm(10)), ncol = 2))
res.R2 <- evalRandVar(R2, X)
res.R2[3,,1] # results for Map(R2)[[3]](X[,1])
Map(log(abs(R2))) # "Math" group generic
# "Arith" group generic
Map(3 + R1)
Map(c(1,3,5) * R1)
try(1:5 * R1) # error
Map(1:2 * R2)
Map(R2 - 5)
Map(R1 ^ R1)
Results
R version 3.3.1 (2016-06-21) -- "Bug in Your Hair"
Copyright (C) 2016 The R Foundation for Statistical Computing
Platform: x86_64-pc-linux-gnu (64-bit)
R is free software and comes with ABSOLUTELY NO WARRANTY.
You are welcome to redistribute it under certain conditions.
Type 'license()' or 'licence()' for distribution details.
R is a collaborative project with many contributors.
Type 'contributors()' for more information and
'citation()' on how to cite R or R packages in publications.
Type 'demo()' for some demos, 'help()' for on-line help, or
'help.start()' for an HTML browser interface to help.
Type 'q()' to quit R.
> library(RandVar)
Loading required package: distr
Loading required package: startupmsg
:startupmsg> Utilities for Start-Up Messages (version 0.9.3)
:startupmsg>
:startupmsg> For more information see ?"startupmsg",
:startupmsg> NEWS("startupmsg")
Loading required package: sfsmisc
Loading required package: SweaveListingUtils
:SweaveListingUtils> Utilities for Sweave Together with
:SweaveListingUtils> TeX 'listings' Package (version
:SweaveListingUtils> 0.7.5)
:SweaveListingUtils>
:SweaveListingUtils> NOTE: Support for this package
:SweaveListingUtils> will stop soon.
:SweaveListingUtils>
:SweaveListingUtils> Package 'knitr' is providing the
:SweaveListingUtils> same functionality in a better
:SweaveListingUtils> way.
:SweaveListingUtils>
:SweaveListingUtils> Some functions from package 'base'
:SweaveListingUtils> are intentionally masked ---see
:SweaveListingUtils> SweaveListingMASK().
:SweaveListingUtils>
:SweaveListingUtils> Note that global options are
:SweaveListingUtils> controlled by
:SweaveListingUtils> SweaveListingoptions() ---c.f.
:SweaveListingUtils> ?"SweaveListingoptions".
:SweaveListingUtils>
:SweaveListingUtils> For more information see
:SweaveListingUtils> ?"SweaveListingUtils",
:SweaveListingUtils> NEWS("SweaveListingUtils")
:SweaveListingUtils> There is a vignette to this
:SweaveListingUtils> package; try
:SweaveListingUtils> vignette("ExampleSweaveListingUtils").
Attaching package: 'SweaveListingUtils'
The following objects are masked from 'package:base':
library, require
:distr> Object Oriented Implementation of Distributions (version
:distr> 2.6)
:distr>
:distr> Attention: Arithmetics on distribution objects are
:distr> understood as operations on corresponding random variables
:distr> (r.v.s); see distrARITH().
:distr>
:distr> Some functions from package 'stats' are intentionally masked
:distr> ---see distrMASK().
:distr>
:distr> Note that global options are controlled by distroptions()
:distr> ---c.f. ?"distroptions".
:distr>
:distr> For more information see ?"distr", NEWS("distr"), as well as
:distr> http://distr.r-forge.r-project.org/
:distr> Package "distrDoc" provides a vignette to this package as
:distr> well as to several extension packages; try
:distr> vignette("distr").
Attaching package: 'distr'
The following objects are masked from 'package:stats':
df, qqplot, sd
Loading required package: distrEx
:distrEx> Extensions of Package 'distr' (version 2.6)
:distrEx>
:distrEx> Note: Packages "e1071", "moments", "fBasics" should be
:distrEx> attached /before/ package "distrEx". See
:distrEx> distrExMASK().Note: Extreme value distribution
:distrEx> functionality has been moved to
:distrEx>
:distrEx> package "RobExtremes". See distrExMOVED().
:distrEx>
:distrEx> For more information see ?"distrEx", NEWS("distrEx"), as
:distrEx> well as
:distrEx> http://distr.r-forge.r-project.org/
:distrEx> Package "distrDoc" provides a vignette to this package
:distrEx> as well as to several related packages; try
:distrEx> vignette("distr").
Attaching package: 'distrEx'
The following objects are masked from 'package:stats':
IQR, mad, median, var
:RandVar> Implementation of Random Variables (version 1.0)
:RandVar>
:RandVar> For more information see ?"RandVar", NEWS("RandVar"), as
:RandVar> well as
:RandVar> http://robast.r-forge.r-project.org/
:RandVar> This package also includes a vignette; try
:RandVar> vignette("RandVar").
> png(filename="/home/ddbj/snapshot/RGM3/R_CC/result/RandVar/EuclRandVariable-class.Rd_%03d_medium.png", width=480, height=480)
> ### Name: EuclRandVariable-class
> ### Title: Euclidean random variable
> ### Aliases: EuclRandVariable-class
> ### coerce,EuclRandVariable,EuclRandMatrix-method
> ### coerce,EuclRandVariable,EuclRandVarList-method
> ### Range<-,EuclRandVariable-method [,EuclRandVariable-method evalRandVar
> ### evalRandVar,EuclRandVariable,numeric,missing-method
> ### evalRandVar,EuclRandVariable,matrix,missing-method
> ### evalRandVar,EuclRandVariable,numeric,Distribution-method
> ### evalRandVar,EuclRandVariable,matrix,Distribution-method imageDistr
> ### imageDistr,EuclRandVariable,Distribution-method
> ### dimension,EuclRandVariable-method t,EuclRandVariable-method
> ### %*%,matrix,EuclRandVariable-method
> ### %*%,numeric,EuclRandVariable-method
> ### %*%,EuclRandVariable,matrix-method
> ### %*%,EuclRandVariable,numeric-method
> ### %*%,EuclRandVariable,EuclRandVariable-method
> ### %*%,EuclRandVariable,EuclRandMatrix-method
> ### %*%,EuclRandMatrix,EuclRandVariable-method
> ### Arith,numeric,EuclRandVariable-method
> ### Arith,EuclRandVariable,numeric-method
> ### Arith,EuclRandVariable,EuclRandVariable-method
> ### Math,EuclRandVariable-method
> ### E,UnivariateDistribution,EuclRandVariable,missing-method
> ### E,AbscontDistribution,EuclRandVariable,missing-method
> ### E,DiscreteDistribution,EuclRandVariable,missing-method
> ### E,MultivariateDistribution,EuclRandVariable,missing-method
> ### E,DiscreteMVDistribution,EuclRandVariable,missing-method
> ### E,UnivariateCondDistribution,EuclRandVariable,numeric-method
> ### E,AbscontCondDistribution,EuclRandVariable,numeric-method
> ### E,DiscreteCondDistribution,EuclRandVariable,numeric-method
> ### Keywords: classes arith math
>
> ### ** Examples
>
> L1 <- list(function(x){x}, function(x){x^2}, function(x){x^3}, function(x){x^4})
> L2 <- list(function(x){exp(x)}, function(x){abs(x)},
+ function(x){sin(x)}, function(x){floor(x)})
>
> R1 <- new("EuclRandVariable", Map = L1, Domain = Reals(), Range = Reals())
> dimension(R1)
[1] 4
> Map(R1)
[[1]]
function (x)
{
x
}
[[2]]
function (x)
{
x^2
}
[[3]]
function (x)
{
x^3
}
[[4]]
function (x)
{
x^4
}
> Range(R1)
An object of class "Reals"
Slot "dimension":
[1] 1
Slot "name":
[1] "Real Space"
> R1[2]
An object of class "EuclRandVariable"
length of Map: 1
Domain: Real Space with dimension 1
Range: Real Space with dimension 1
> Map(R1[3])
[[1]]
function (x)
{
x^3
}
> Map(R1[c(1,2,4)])
[[1]]
function (x)
{
x
}
[[2]]
function (x)
{
x^2
}
[[3]]
function (x)
{
x^4
}
> Map(R1[2:4])
[[1]]
function (x)
{
x^2
}
[[2]]
function (x)
{
x^3
}
[[3]]
function (x)
{
x^4
}
> set.seed(123)
> evalRandVar(R1, rnorm(1))
[,1]
[1,] -0.56047565
[2,] 0.31413295
[3,] -0.17606387
[4,] 0.09867951
> x <- as.matrix(rnorm(10))
> res.R1 <- evalRandVar(R1, x)
> res.R1[2,,] # results for Map(R1)[[2]](x)
[1] 0.052981677 2.429571609 0.004971433 0.016715318 2.941447909 0.212443749
[7] 1.600379927 0.471766840 0.198614592 1.498376247
> res.R1[2,1,] # results for Map(R1)[[2]](x[1,])
[1] 0.05298168
>
> R2 <- EuclRandVariable(L2, Domain = Reals(), dimension = 1)
> dimension(R2)
[1] 4
> DL1 <- imageDistr(R2, Norm())
> plot(DL1)
>
> Domain(R2) <- EuclideanSpace(dimension = 2)
> Range(R2) <- EuclideanSpace(dimension = 2)
> dimension(R2)
[1] 8
> (X <- matrix(c(x, rnorm(10)), ncol = 2))
[,1] [,2]
[1,] -0.23017749 0.3598138
[2,] 1.55870831 0.4007715
[3,] 0.07050839 0.1106827
[4,] 0.12928774 -0.5558411
[5,] 1.71506499 1.7869131
[6,] 0.46091621 0.4978505
[7,] -1.26506123 -1.9666172
[8,] -0.68685285 0.7013559
[9,] -0.44566197 -0.4727914
[10,] 1.22408180 -1.0678237
> res.R2 <- evalRandVar(R2, X)
> res.R2[3,,1] # results for Map(R2)[[3]](X[,1])
[1] -0.22815034 0.99992694 0.07044998 0.12892786 0.98961131 0.44476889
[7] -0.95362595 -0.63410681 -0.43105529 0.94049422
>
> Map(log(abs(R2))) # "Math" group generic
[[1]]
function (x)
{
f1 <- function (x)
{
f1 <- function (x)
{
exp(x)
}
abs(f1(x))
}
log(f1(x))
}
<environment: 0x6e9f798>
[[2]]
function (x)
{
f1 <- function (x)
{
f1 <- function (x)
{
abs(x)
}
abs(f1(x))
}
log(f1(x))
}
<environment: 0x6e9f798>
[[3]]
function (x)
{
f1 <- function (x)
{
f1 <- function (x)
{
sin(x)
}
abs(f1(x))
}
log(f1(x))
}
<environment: 0x6e9f798>
[[4]]
function (x)
{
f1 <- function (x)
{
f1 <- function (x)
{
floor(x)
}
abs(f1(x))
}
log(f1(x))
}
<environment: 0x6e9f798>
>
> # "Arith" group generic
> Map(3 + R1)
[[1]]
function (x)
{
f2 <- function (x)
{
x
}
3 + f2(x)
}
<environment: 0x6e7cc38>
[[2]]
function (x)
{
f2 <- function (x)
{
x^2
}
3 + f2(x)
}
<environment: 0x6e7cc38>
[[3]]
function (x)
{
f2 <- function (x)
{
x^3
}
3 + f2(x)
}
<environment: 0x6e7cc38>
[[4]]
function (x)
{
f2 <- function (x)
{
x^4
}
3 + f2(x)
}
<environment: 0x6e7cc38>
> Map(c(1,3,5) * R1)
[[1]]
function (x)
{
f2 <- function (x)
{
x
}
1 * f2(x)
}
<environment: 0x6e53748>
[[2]]
function (x)
{
f2 <- function (x)
{
x^2
}
3 * f2(x)
}
<environment: 0x6e53748>
[[3]]
function (x)
{
f2 <- function (x)
{
x^3
}
5 * f2(x)
}
<environment: 0x6e53748>
[[4]]
function (x)
{
f2 <- function (x)
{
x^4
}
1 * f2(x)
}
<environment: 0x6e53748>
Warning message:
In c(1, 3, 5) * R1 :
longer object length is not a multiple of shorter object length
> try(1:5 * R1) # error
Error in 1:5 * R1 :
length of 'numeric' has to be less or equal dimension of 'EuclRandVariable'
> Map(1:2 * R2)
[[1]]
function (x)
{
f2 <- function (x)
{
exp(x)
}
1:2 * f2(x)
}
<environment: 0x6df3028>
[[2]]
function (x)
{
f2 <- function (x)
{
abs(x)
}
1:2 * f2(x)
}
<environment: 0x6df3028>
[[3]]
function (x)
{
f2 <- function (x)
{
sin(x)
}
1:2 * f2(x)
}
<environment: 0x6df3028>
[[4]]
function (x)
{
f2 <- function (x)
{
floor(x)
}
1:2 * f2(x)
}
<environment: 0x6df3028>
> Map(R2 - 5)
[[1]]
function (x)
{
f1 <- function (x)
{
exp(x)
}
f1(x) - c(5, 5)
}
<environment: 0x6dcdee8>
[[2]]
function (x)
{
f1 <- function (x)
{
abs(x)
}
f1(x) - c(5, 5)
}
<environment: 0x6dcdee8>
[[3]]
function (x)
{
f1 <- function (x)
{
sin(x)
}
f1(x) - c(5, 5)
}
<environment: 0x6dcdee8>
[[4]]
function (x)
{
f1 <- function (x)
{
floor(x)
}
f1(x) - c(5, 5)
}
<environment: 0x6dcdee8>
> Map(R1 ^ R1)
[[1]]
function (x)
{
f1 <- function (x)
{
x
}
f2 <- function (x)
{
x
}
f1(x)^f2(x)
}
<environment: 0x6da7080>
[[2]]
function (x)
{
f1 <- function (x)
{
x^2
}
f2 <- function (x)
{
x^2
}
f1(x)^f2(x)
}
<environment: 0x6da7080>
[[3]]
function (x)
{
f1 <- function (x)
{
x^3
}
f2 <- function (x)
{
x^3
}
f1(x)^f2(x)
}
<environment: 0x6da7080>
[[4]]
function (x)
{
f1 <- function (x)
{
x^4
}
f2 <- function (x)
{
x^4
}
f1(x)^f2(x)
}
<environment: 0x6da7080>
>
>
>
>
>
>
> dev.off()
null device
1
>
|