Last data update: 2014.03.03

 R: Maximum Pseudo-Likelihood Estimation of 1-Dim SDE
fitsdeR Documentation

Maximum Pseudo-Likelihood Estimation of 1-Dim SDE

Description

The (S3) generic function "fitsde" of estimate drift and diffusion parameters by the method of maximum pseudo-likelihood of the 1-dim stochastic differential equation.

Usage

fitsde(data, ...)
## Default S3 method:
fitsde(data, drift, diffusion, start = list(), pmle = c("euler","kessler", 
   "ozaki", "shoji"), optim.method = "L-BFGS-B",
   lower = -Inf, upper = Inf, ...)
   
## S3 method for class 'fitsde'
summary(object, ...)
## S3 method for class 'fitsde'
coef(object, ...)
## S3 method for class 'fitsde'
vcov(object, ...)
## S3 method for class 'fitsde'
logLik(object, ...)
## S3 method for class 'fitsde'
AIC(object, ...)
## S3 method for class 'fitsde'
BIC(object, ...)
## S3 method for class 'fitsde'
confint(object,parm, level=0.95, ...)

Arguments

data

a univariate time series (ts class).

drift

drift coefficient: an expression of two variables t, x and theta a vector of parameters of sde. See Examples.

diffusion

diffusion coefficient: an expression of two variables t, x and theta a vector of parameters of sde. See Examples.

start

named list of starting values for optimizer. See Examples.

pmle

a character string specifying the method; can be either: "euler" (Euler pseudo-likelihood), "ozaki" (Ozaki pseudo-likelihood), "shoji" (Shoji pseudo-likelihood), and "kessler" (Kessler pseudo-likelihood).

optim.method

the method for optim.

lower, upper

bounds on the variables for the "Brent" or "L-BFGS-B" method.

object

an object inheriting from class "fitsde".

parm

a specification of which parameters are to be given confidence intervals, either a vector of names (example parm='theta1'). If missing, all parameters are considered.

level

the confidence level required.

...

further arguments to pass to optim.

Details

The function fitsde returns a pseudo-likelihood estimators of the drift and diffusion parameters in 1-dim stochastic differential equation. The optim optimizer is used to find the maximum of the negative log pseudo-likelihood. An approximate covariance matrix for the parameters is obtained by inverting the Hessian matrix at the optimum.

The pmle of pseudo-likelihood can be one among:"euler": Euler pseudo-likelihood), "ozaki": Ozaki pseudo-likelihood, "shoji": Shoji pseudo-likelihood, and "kessler": Kessler pseudo-likelihood.

For more details see vignette("FitSDE").

Value

fitsde returns an object inheriting from class "fitsde".

Author(s)

A.C. Guidoum, K. Boukhetala.

References

Kessler, M. (1997). Estimation of an ergodic diffusion from discrete observations. Scand. J. Statist., 24, 211-229.

Iacus, S.M. (2008). Simulation and inference for stochastic differential equations: with R examples. Springer-Verlag, New York.

Iacus, S.M. (2009). sde: Simulation and Inference for Stochastic Differential Equations. R package version 2.0.10.

Iacus, S.M. and all. (2014). The yuima Project: A Computational Framework for Simulation and Inference of Stochastic Differential Equations. Journal of Statistical Software, 57(4).

Ozaki, T. (1992). A bridge between nonlinear time series models and nonlinear stochastic dynamical systems: A local linearization approach. Statistica Sinica, 2, 25-83.

Shoji, L., Ozaki, T. (1998). Estimation for nonlinear stochastic differential equations by a local linearization method. Stochastic Analysis and Applications, 16, 733-752.

Dacunha, D.C. and Florens, D.Z. (1986). Estimation of the Coefficients of a Diffusion from Discrete Observations. Stochastics. 19, 263–284.

Dohnal, G. (1987). On estimating the diffusion coefficient. J. Appl.Prob., 24, 105–114.

Genon, V.C. (1990). Maximum constrast estimation for diffusion processes from discrete observation. Statistics, 21, 99–116.

Nicolau, J. (2004). Introduction to the estimation of stochastic differential equations based on discrete observations. Autumn School and International Conference, Stochastic Finance.

Ait-Sahalia, Y. (1999). Transition densities for interest rate and other nonlinear diffusions. The Journal of Finance, 54, 1361–1395.

Ait-Sahalia, Y. (2002). Maximum likelihood estimation of discretely sampled diffusions: a closed-form approximation approach. Econometrica. 70, 223–262.

B.L.S. Prakasa Rao. (1999). Statistical Inference for Diffusion Type Processes. Arnold, London and Oxford University press, New York.

Kutoyants, Y.A. (2004). Statistical Inference for Ergodic Diffusion Processes. Springer, London.

See Also

dcEuler, dcElerian, dcOzaki, dcShoji, dcKessler and dcSim for approximated conditional law of a diffusion process. gmm estimator of the generalized method of moments by Hansen, and HPloglik these functions are useful to calculate approximated maximum likelihood estimators when the transition density of the process is not known, in package sde.

qmle in package "yuima" calculate quasi-likelihood and ML estimator of least squares estimator.

PSM.estimate in package PSM for estimation of linear and non-linear mixed-effects models using stochastic differential equations.

Examples

#####  Example 1:

## Modele GBM (BS)
## dX(t) = theta1 * X(t) * dt + theta2 * x * dW(t)
## Simulation of data
set.seed(1234)

X <- GBM(N =1000,theta=4,sigma=1)
## Estimation: true theta=c(4,1)
fx <- expression(theta[1]*x)
gx <- expression(theta[2]*x)

fres <- fitsde(data=X,drift=fx,diffusion=gx,start = list(theta1=1,theta2=1),
              lower=c(0,0))
fres			   
summary(fres)
coef(fres)
logLik(fres)
AIC(fres)
BIC(fres)
vcov(fres)
confint(fres,level=0.95)


#####  Example 2:


## Nonlinear mean reversion (Ait-Sahalia) modele
## dX(t) = (theta1 + theta2*x + theta3*x^2) * dt + theta4 * x^theta5 * dW(t) 
## Simulation of the process X(t)
set.seed(1234)

f <- expression(1 - 11*x + 2*x^2)
g <- expression(x^0.5)
res <- snssde1d(drift=f,diffusion=g,M=1,N=1000,Dt=0.001,x0=5)
mydata1 <- res$X

## Estimation
## true param theta= c(1,-11,2,1,0.5)
true <- c(1,-11,2,1,0.5)
pmle <- eval(formals(fitsde.default)$pmle)

fx <- expression(theta[1] + theta[2]*x + theta[3]*x^2)
gx <- expression(theta[4]*x^theta[5])

fres <- lapply(1:4, function(i) fitsde(mydata1,drift=fx,diffusion=gx,
	             pmle=pmle[i],start = list(theta1=1,theta2=1,theta3=1,theta4=1,
                 theta5=1),optim.method = "L-BFGS-B"))
Coef <- data.frame(true,do.call("cbind",lapply(1:4,function(i) coef(fres[[i]]))))
names(Coef) <- c("True",pmle)
Summary <- data.frame(do.call("rbind",lapply(1:4,function(i) logLik(fres[[i]]))),
                      do.call("rbind",lapply(1:4,function(i) AIC(fres[[i]]))),
                      do.call("rbind",lapply(1:4,function(i) BIC(fres[[i]]))),
                      row.names=pmle)
names(Summary) <- c("logLik","AIC","BIC")
Coef	
Summary


#####  Example 3:

## dX(t) = (theta1*x*t+theta2*tan(x)) *dt + theta3*t *dW(t)
## Simulation of data
set.seed(1234)

f <- expression(2*x*t-tan(x))
g <- expression(1.25*t)
sim <- snssde1d(drift=f,diffusion=g,M=1,N=1000,Dt=0.001,x0=10)
mydata2 <- sim$X

## Estimation
## true param theta= c(2,-1,1.25)
true <- c(2,-1,1.25)

fx <- expression(theta[1]*x*t+theta[2]*tan(x))
gx <- expression(theta[3]*t)

fres <- lapply(1:4, function(i) fitsde(mydata2,drift=fx,diffusion=gx,
	             pmle=pmle[i],start = list(theta1=1,theta2=1,theta3=1),
				 optim.method = "L-BFGS-B"))
Coef <- data.frame(true,do.call("cbind",lapply(1:4,function(i) coef(fres[[i]]))))
names(Coef) <- c("True",pmle)
Summary <- data.frame(do.call("rbind",lapply(1:4,function(i) logLik(fres[[i]]))),
                      do.call("rbind",lapply(1:4,function(i) AIC(fres[[i]]))),
                      do.call("rbind",lapply(1:4,function(i) BIC(fres[[i]]))),
                      row.names=pmle)
names(Summary) <- c("logLik","AIC","BIC")
Coef
Summary		


#####  Example 4:

## Application to real data
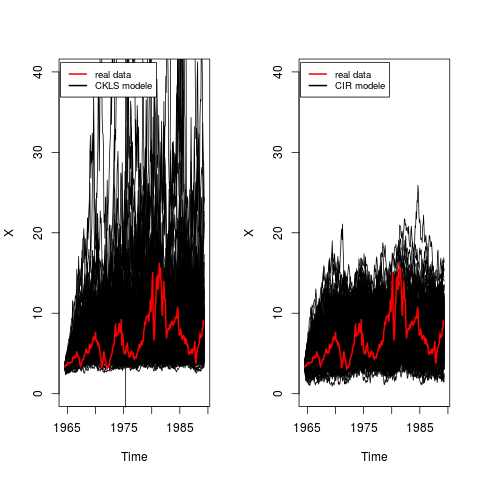
## CKLS modele vs CIR modele 
## CKLS (mod1):  dX(t) = (theta1+theta2* X(t))* dt + theta3 * X(t)^theta4 * dW(t)
## CIR  (mod2):  dX(t) = (theta1+theta2* X(t))* dt + theta3 * sqrt(X(t))  * dW(t)
set.seed(1234)

data(Irates)
rates <- Irates[,"r1"]
rates <- window(rates, start=1964.471, end=1989.333)

fx1 <- expression(theta[1]+theta[2]*x)
gx1 <- expression(theta[3]*x^theta[4])
gx2 <- expression(theta[3]*sqrt(x))

fitmod1 <- fitsde(rates,drift=fx1,diffusion=gx1,pmle="euler",start = list(theta1=1,theta2=1,
                  theta3=1,theta4=1),optim.method = "L-BFGS-B")
fitmod2 <- fitsde(rates,drift=fx1,diffusion=gx2,pmle="euler",start = list(theta1=1,theta2=1,
                  theta3=1),optim.method = "L-BFGS-B")	
summary(fitmod1)
summary(fitmod2)
coef(fitmod1)
coef(fitmod2)
confint(fitmod1,parm=c('theta2','theta3'))
confint(fitmod2,parm=c('theta2','theta3'))
AIC(fitmod1)
AIC(fitmod2)	

## Display
## CKLS Modele
op <- par(mfrow = c(1, 2))
theta <- coef(fitmod1)
N <- length(rates)
res <- snssde1d(drift=fx1,diffusion=gx1,M=200,t0=time(rates)[1],T=time(rates)[N],
                Dt=deltat(rates),x0=rates[1],N)
plot(res,plot.type="single",ylim=c(0,40))
lines(rates,col=2,lwd=2)
legend("topleft",c("real data","CKLS modele"),inset = .01,col=c(2,1),lwd=2,cex=0.8)

## CIR Modele
theta <- coef(fitmod2)
res <- snssde1d(drift=fx1,diffusion=gx2,M=200,t0=time(rates)[1],T=time(rates)[N],
                Dt=deltat(rates),x0=rates[1],N)
plot(res,plot.type="single",ylim=c(0,40))
lines(rates,col=2,lwd=2)
legend("topleft",c("real data","CIR modele"),inset = .01,col=c(2,1),lwd=2,cex=0.8)
par(op)

Results


R version 3.3.1 (2016-06-21) -- "Bug in Your Hair"
Copyright (C) 2016 The R Foundation for Statistical Computing
Platform: x86_64-pc-linux-gnu (64-bit)

R is free software and comes with ABSOLUTELY NO WARRANTY.
You are welcome to redistribute it under certain conditions.
Type 'license()' or 'licence()' for distribution details.

R is a collaborative project with many contributors.
Type 'contributors()' for more information and
'citation()' on how to cite R or R packages in publications.

Type 'demo()' for some demos, 'help()' for on-line help, or
'help.start()' for an HTML browser interface to help.
Type 'q()' to quit R.

> library(Sim.DiffProc)
Package 'Sim.DiffProc' version 3.2 loaded.
help(Sim.DiffProc) for summary information.
> png(filename="/home/ddbj/snapshot/RGM3/R_CC/result/Sim.DiffProc/fitsde.Rd_%03d_medium.png", width=480, height=480)
> ### Name: fitsde
> ### Title: Maximum Pseudo-Likelihood Estimation of 1-Dim SDE
> ### Aliases: fitsde fitsde.default summary.fitsde print.fitsde vcov.fitsde
> ###   AIC.fitsde BIC.fitsde logLik.fitsde coef.fitsde confint.fitsde
> ### Keywords: fit ts sde
> 
> ### ** Examples
> 
> #####  Example 1:
> 
> ## Modele GBM (BS)
> ## dX(t) = theta1 * X(t) * dt + theta2 * x * dW(t)
> ## Simulation of data
> set.seed(1234)
> 
> X <- GBM(N =1000,theta=4,sigma=1)
> ## Estimation: true theta=c(4,1)
> fx <- expression(theta[1]*x)
> gx <- expression(theta[2]*x)
> 
> fres <- fitsde(data=X,drift=fx,diffusion=gx,start = list(theta1=1,theta2=1),
+               lower=c(0,0))
> fres			   

Call:
fitsde(data = X, drift = fx, diffusion = gx, start = list(theta1 = 1, 
    theta2 = 1), lower = c(0, 0))

Coefficients:
  theta1   theta2 
3.160720 1.000225 
> summary(fres)
Pseudo maximum likelihood estimation

Method:  Euler
Call:
fitsde(data = X, drift = fx, diffusion = gx, start = list(theta1 = 1, 
    theta2 = 1), lower = c(0, 0))

Coefficients:
       Estimate Std. Error
theta1 3.160720 1.00022484
theta2 1.000225 0.02236563

-2 log L: -1330.008 
> coef(fres)
  theta1   theta2 
3.160720 1.000225 
> logLik(fres)
[1] 665.004
> AIC(fres)
[1] -1326.008
> BIC(fres)
[1] -1316.19
> vcov(fres)
              theta1        theta2
theta1  1.000450e+00 -1.385373e-08
theta2 -1.385373e-08  5.002214e-04
> confint(fres,level=0.95)
          2.5 %   97.5 %
theta1 1.200315 5.121125
theta2 0.956389 1.044061
> 
> ## No test: 
> #####  Example 2:
> 
> 
> ## Nonlinear mean reversion (Ait-Sahalia) modele
> ## dX(t) = (theta1 + theta2*x + theta3*x^2) * dt + theta4 * x^theta5 * dW(t) 
> ## Simulation of the process X(t)
> set.seed(1234)
> 
> f <- expression(1 - 11*x + 2*x^2)
> g <- expression(x^0.5)
> res <- snssde1d(drift=f,diffusion=g,M=1,N=1000,Dt=0.001,x0=5)
> mydata1 <- res$X
> 
> ## Estimation
> ## true param theta= c(1,-11,2,1,0.5)
> true <- c(1,-11,2,1,0.5)
> pmle <- eval(formals(fitsde.default)$pmle)
> 
> fx <- expression(theta[1] + theta[2]*x + theta[3]*x^2)
> gx <- expression(theta[4]*x^theta[5])
> 
> fres <- lapply(1:4, function(i) fitsde(mydata1,drift=fx,diffusion=gx,
+ 	             pmle=pmle[i],start = list(theta1=1,theta2=1,theta3=1,theta4=1,
+                  theta5=1),optim.method = "L-BFGS-B"))
> Coef <- data.frame(true,do.call("cbind",lapply(1:4,function(i) coef(fres[[i]]))))
> names(Coef) <- c("True",pmle)
> Summary <- data.frame(do.call("rbind",lapply(1:4,function(i) logLik(fres[[i]]))),
+                       do.call("rbind",lapply(1:4,function(i) AIC(fres[[i]]))),
+                       do.call("rbind",lapply(1:4,function(i) BIC(fres[[i]]))),
+                       row.names=pmle)
> names(Summary) <- c("logLik","AIC","BIC")
> Coef	
        True      euler     kessler       ozaki       shoji
theta1   1.0  0.6873700  0.66607155  0.65115001  0.68374592
theta2 -11.0 -6.9947010 -6.86096214 -6.85205839 -6.92324706
theta3   2.0  0.1152499  0.06059366  0.06270915  0.07623474
theta4   1.0  1.0022594  1.00664000  1.00512419  1.00547899
theta5   0.5  0.5055101  0.50662118  0.50800957  0.50539687
> Summary
          logLik       AIC       BIC
euler   2758.713 -5507.427 -5503.609
kessler 2758.610 -5507.219 -5503.402
ozaki   2758.528 -5507.056 -5503.239
shoji   2758.709 -5507.419 -5503.601
> 
> 
> #####  Example 3:
> 
> ## dX(t) = (theta1*x*t+theta2*tan(x)) *dt + theta3*t *dW(t)
> ## Simulation of data
> set.seed(1234)
> 
> f <- expression(2*x*t-tan(x))
> g <- expression(1.25*t)
> sim <- snssde1d(drift=f,diffusion=g,M=1,N=1000,Dt=0.001,x0=10)
> mydata2 <- sim$X
> 
> ## Estimation
> ## true param theta= c(2,-1,1.25)
> true <- c(2,-1,1.25)
> 
> fx <- expression(theta[1]*x*t+theta[2]*tan(x))
> gx <- expression(theta[3]*t)
> 
> fres <- lapply(1:4, function(i) fitsde(mydata2,drift=fx,diffusion=gx,
+ 	             pmle=pmle[i],start = list(theta1=1,theta2=1,theta3=1),
+ 				 optim.method = "L-BFGS-B"))
Warning messages:
1: In log(1 + (A(t0, x0, theta)/(x0 * Ax(t0, x0, theta))) * (exp(Ax(t0,  :
  NaNs produced
2: In log(1 + (A(t0, x0, theta)/(x0 * Ax(t0, x0, theta))) * (exp(Ax(t0,  :
  NaNs produced
3: In log(1 + (A(t0, x0, theta)/(x0 * Ax(t0, x0, theta))) * (exp(Ax(t0,  :
  NaNs produced
4: In log(1 + (A(t0, x0, theta)/(x0 * Ax(t0, x0, theta))) * (exp(Ax(t0,  :
  NaNs produced
5: In log(1 + (A(t0, x0, theta)/(x0 * Ax(t0, x0, theta))) * (exp(Ax(t0,  :
  NaNs produced
6: In log(1 + (A(t0, x0, theta)/(x0 * Ax(t0, x0, theta))) * (exp(Ax(t0,  :
  NaNs produced
7: In log(1 + (A(t0, x0, theta)/(x0 * Ax(t0, x0, theta))) * (exp(Ax(t0,  :
  NaNs produced
> Coef <- data.frame(true,do.call("cbind",lapply(1:4,function(i) coef(fres[[i]]))))
> names(Coef) <- c("True",pmle)
> Summary <- data.frame(do.call("rbind",lapply(1:4,function(i) logLik(fres[[i]]))),
+                       do.call("rbind",lapply(1:4,function(i) AIC(fres[[i]]))),
+                       do.call("rbind",lapply(1:4,function(i) BIC(fres[[i]]))),
+                       row.names=pmle)
> names(Summary) <- c("logLik","AIC","BIC")
> Coef
        True     euler    kessler      ozaki      shoji
theta1  2.00  1.914026 0.95314362  1.9115444  1.9085177
theta2 -1.00 -0.990799 0.01136956 -0.9897514 -0.9612274
theta3  1.25  1.255735 1.64358954  1.2834434  1.3245215
> Summary		
          logLik       AIC       BIC
euler   2801.036 -5596.073 -5588.255
kessler 2584.406 -5162.812 -5154.994
ozaki   2778.965 -5551.929 -5544.112
shoji   2793.992 -5581.984 -5574.166
> ## End(No test)
> 
> #####  Example 4:
> 
> ## Application to real data
> ## CKLS modele vs CIR modele 
> ## CKLS (mod1):  dX(t) = (theta1+theta2* X(t))* dt + theta3 * X(t)^theta4 * dW(t)
> ## CIR  (mod2):  dX(t) = (theta1+theta2* X(t))* dt + theta3 * sqrt(X(t))  * dW(t)
> set.seed(1234)
> 
> data(Irates)
> rates <- Irates[,"r1"]
> rates <- window(rates, start=1964.471, end=1989.333)
> 
> fx1 <- expression(theta[1]+theta[2]*x)
> gx1 <- expression(theta[3]*x^theta[4])
> gx2 <- expression(theta[3]*sqrt(x))
> 
> fitmod1 <- fitsde(rates,drift=fx1,diffusion=gx1,pmle="euler",start = list(theta1=1,theta2=1,
+                   theta3=1,theta4=1),optim.method = "L-BFGS-B")
> fitmod2 <- fitsde(rates,drift=fx1,diffusion=gx2,pmle="euler",start = list(theta1=1,theta2=1,
+                   theta3=1),optim.method = "L-BFGS-B")	
> summary(fitmod1)
Pseudo maximum likelihood estimation

Method:  Euler
Call:
fitsde(data = rates, drift = fx1, diffusion = gx1, pmle = "euler", 
    start = list(theta1 = 1, theta2 = 1, theta3 = 1, theta4 = 1), 
    optim.method = "L-BFGS-B")

Coefficients:
         Estimate Std. Error
theta1  2.0769516 0.98838467
theta2 -0.2631871 0.19544290
theta3  0.1302158 0.02523105
theta4  1.4513173 0.10323740

-2 log L: 475.7572 
> summary(fitmod2)
Pseudo maximum likelihood estimation

Method:  Euler
Call:
fitsde(data = rates, drift = fx1, diffusion = gx2, pmle = "euler", 
    start = list(theta1 = 1, theta2 = 1, theta3 = 1), optim.method = "L-BFGS-B")

Coefficients:
         Estimate Std. Error
theta1  2.6387593 1.18754725
theta2 -0.3606083 0.18896205
theta3  0.8650745 0.03549428

-2 log L: 563.7025 
> coef(fitmod1)
    theta1     theta2     theta3     theta4 
 2.0769516 -0.2631871  0.1302158  1.4513173 
> coef(fitmod2)
    theta1     theta2     theta3 
 2.6387593 -0.3606083  0.8650745 
> confint(fitmod1,parm=c('theta2','theta3'))
             2.5 %    97.5 %
theta2 -0.64624812 0.1198740
theta3  0.08076388 0.1796678
> confint(fitmod2,parm=c('theta2','theta3'))
            2.5 %      97.5 %
theta2 -0.7309671 0.009750478
theta3  0.7955070 0.934642013
> AIC(fitmod1)
[1] 483.7572
> AIC(fitmod2)	
[1] 569.7025
> ## No test: 
> ## Display
> ## CKLS Modele
> op <- par(mfrow = c(1, 2))
> theta <- coef(fitmod1)
> N <- length(rates)
> res <- snssde1d(drift=fx1,diffusion=gx1,M=200,t0=time(rates)[1],T=time(rates)[N],
+                 Dt=deltat(rates),x0=rates[1],N)
> plot(res,plot.type="single",ylim=c(0,40))
> lines(rates,col=2,lwd=2)
> legend("topleft",c("real data","CKLS modele"),inset = .01,col=c(2,1),lwd=2,cex=0.8)
> 
> ## CIR Modele
> theta <- coef(fitmod2)
> res <- snssde1d(drift=fx1,diffusion=gx2,M=200,t0=time(rates)[1],T=time(rates)[N],
+                 Dt=deltat(rates),x0=rates[1],N)
> plot(res,plot.type="single",ylim=c(0,40))
> lines(rates,col=2,lwd=2)
> legend("topleft",c("real data","CIR modele"),inset = .01,col=c(2,1),lwd=2,cex=0.8)
> par(op)  
> ## End(No test)			  
> 
> 
> 
> 
> 
> dev.off()
null device 
          1 
>


Created & Maintained by Osamu Ogasawara (osamu.ogasawara@gmail.com) and IMSBIO