Supported by Dr. Osamu Ogasawara and  providing providing  . . |
|
Last data update: 2014.03.03 |
Range of a normal inverse Gaussian DistributionDescriptionGiven the parameter vector param of a normal inverse Gaussian distribution,
this function calculates the range outside of which the distribution
has negligible probability, or the density function is negligible, to
a specified tolerance. The parameterization used
is the (alpha, beta) one (see
Usage
nigCalcRange(mu = 0, delta = 1, alpha = 1, beta = 0,
param = c(mu, delta, alpha, beta),
tol = 10^(-5), density = TRUE, ...)
Arguments
DetailsThe particular normal inverse Gaussian distribution being considered is
specified by the parameter value If If ValueA two-component vector giving the lower and upper ends of the range. Author(s)David Scott d.scott@auckland.ac.nz, Christine Yang Dong ReferencesBarndorff-Nielsen, O. and Bl<c3><a6>sild, P (1983). Hyperbolic distributions. In Encyclopedia of Statistical Sciences, eds., Johnson, N. L., Kotz, S. and Read, C. B., Vol. 3, pp. 700–707. New York: Wiley. Paolella, Marc S. (2007) Intermediate Probability: A Computational Approach, Chichester: Wiley See Also
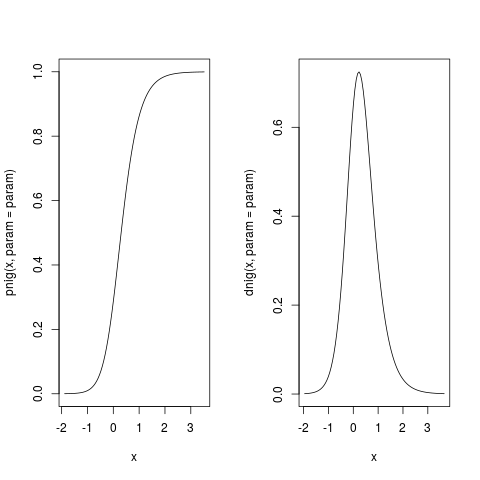
Examplespar(mfrow = c(1, 2)) param <- c(0, 1, 3, 1) nigRange <- nigCalcRange(param = param, tol = 10^(-3)) nigRange curve(pnig(x, param = param), nigRange[1], nigRange[2]) maxDens <- dnig(nigMode(param = param), param = param) nigRange <- nigCalcRange(param = param, tol = 10^(-3) * maxDens, density = TRUE) nigRange curve(dnig(x, param = param), nigRange[1], nigRange[2]) Results
R version 3.3.1 (2016-06-21) -- "Bug in Your Hair"
Copyright (C) 2016 The R Foundation for Statistical Computing
Platform: x86_64-pc-linux-gnu (64-bit)
R is free software and comes with ABSOLUTELY NO WARRANTY.
You are welcome to redistribute it under certain conditions.
Type 'license()' or 'licence()' for distribution details.
R is a collaborative project with many contributors.
Type 'contributors()' for more information and
'citation()' on how to cite R or R packages in publications.
Type 'demo()' for some demos, 'help()' for on-line help, or
'help.start()' for an HTML browser interface to help.
Type 'q()' to quit R.
> library(GeneralizedHyperbolic)
Loading required package: DistributionUtils
Loading required package: RUnit
> png(filename="/home/ddbj/snapshot/RGM3/R_CC/result/GeneralizedHyperbolic/nigCalcRange.Rd_%03d_medium.png", width=480, height=480)
> ### Name: nigCalcRange
> ### Title: Range of a normal inverse Gaussian Distribution
> ### Aliases: nigCalcRange
> ### Keywords: distribution
>
> ### ** Examples
>
> par(mfrow = c(1, 2))
> param <- c(0, 1, 3, 1)
> nigRange <- nigCalcRange(param = param, tol = 10^(-3))
> nigRange
[1] -1.884467 3.518054
> curve(pnig(x, param = param), nigRange[1], nigRange[2])
> maxDens <- dnig(nigMode(param = param), param = param)
> nigRange <- nigCalcRange(param = param, tol = 10^(-3) * maxDens, density = TRUE)
> nigRange
[1] -1.959399 3.658918
> curve(dnig(x, param = param), nigRange[1], nigRange[2])
>
>
>
>
>
> dev.off()
null device
1
>
|