Lilliefors-corrected Kolmogorov-Smirnoff Goodness-Of-Fit Test

Description

Implements the Lilliefors-corrected Kolmogorov-Smirnoff test for use in goodness-of-fit tests, suitable when population parameters are unknown and must be estimated by sample statistics. It uses Monte Carlo simulation to estimate p-values. Coded to wrap around ks.test, it can be used with a variety of continuous distributions, including normal, lognormal, univariate mixtures of normals, uniform, loguniform, exponential, gamma, and Weibull distributions.

Usage

LcKS(x, cdf, nreps = 4999, G = 1:9)

Arguments

Details

The function builds a simulation distribution D.sim of length nreps by drawing random samples from the specified continuous distribution function cdf with parameters calculated from the provided sample x. Observed statistic D and simulated test statistics are calculated using ks.test.

The default nreps=4999 provides accurate p-values. nreps=1999 is sufficient for most cases, and computationally faster when dealing with more complicated distributions (such as univariate normal mixtures, gamma, and Weibull).

The p-value is calculated as the number of Monte Carlo samples with test statistics D as extreme as or more extreme than that in the observed sample D.obs, divided by the nreps number of Monte Carlo samples. A value of 1 is added to both the numerator and denominator to allow the observed sample to be represented within the null distribution (Manly 2004); this has the benefit of avoiding nonsensical p.value=0.000 and accounts for the fact that the p-value is an estimate.

Parameter estimates are calculated for the specified continuous distribution, using maximum-likelihood estimates. When testing against the gamma and Weibull distributions, MASS::fitdistr is used to calculate parameter estimates using maximum likelihood optimization, with sensible starting values. Because this incorporates an optimization routine, the simulation algorithm can be slow if using large nreps or problematic samples. Warnings often occur during these optimizations, caused by difficulties estimating sample statistic standard errors. Because such SEs are not used in the Lilliefors-corrected simulation algorithm, warnings are suppressed during these optimizations.

Sample statistics for the (univariate) normal mixture distribution pmixnorm are calculated using package mclust, which uses BIC to identify the optimal mixture model for the sample, and the EM algorithm to calculate parameter estimates for this model. The number of mixture components G (with default allowing up to 9 components), variance model (whether equal E or variable V variance), and component statistics (means, sds, and mixing proportions pro) are estimated from the sample when calculating D.obs and passed internally when creating random Monte Carlo samples. It is possible that some of these samples may differ in their optimal G (for example a two-component input sample might yield a three-component random sample within the simulation distribution). This can be constrained by specifying that simulation BIC-optimizations only consider G mixture components.

Be aware that constraining G changes the null hypothesis. The default (G=1:9) null hypothesis is that a sample was drawn from any G=1:9-component mixture distribution. Specifying a particular value, such as G=2, restricts the null hypothesis to particular mixture distributions with just G components, even if simulated samples might better be represented as different mixture models.

The LcKS(cdf="pmixnorm") test implements two control loops to avoid errors caused by this constraint and when working with problematic samples. The first loop occurs during model-selection for the observed sample x, and allows for estimation of parameters for the second-best model when those for the optimal model are not able to be calculated by the EM algorithm. A second loop occurs during the simulation algorithm, rejecting samples that cannot be fit by the mixture model specified by the observed sample x. Such problematic cases are most common when the observed or simulated samples have a component(s) with very small variance (i.e., duplicate observations) or when a Monte Carlo sample cannot be fit by the specified G.

Value

A list containing the following components:

Note

The Kolmogorov-Smirnoff (such as ks.test) is only valid as a goodness-of-fit test when the population parameters are known. This is typically not the case in practice. This invalidation occurs because estimating the parameters changes the null distribution of the test statistic; i.e., using the sample to estimate population parameters brings the Kolmogorov-Smirnoff test statistic D closer to the null distribution than it would be under the hypothesis where the population parameters are known (Gihman 1952). In other words, it is biased and results in increased Type II error rates. Lilliefors (1967, 1969) provided a solution, using Monte Carlo simulation to approximate the shape of the null distribution when the sample statistics are used to estimate population parameters, and to use this null distribution as the basis for critical values. The function LcKS generalizes this solution for a range of continuous distributions.

Author(s)

Phil Novack-Gottshall pnovack-gottshall@ben.edu, based on code from Charles Geyer (University of Minnesota).

References

Gihman, I. I. 1952. Ob empiriceskoj funkcii raspredelenija slucaje grouppirovki dannych [On the empirical distribution function in the case of grouping of observations]. Doklady Akademii Nauk SSSR 82: 837-840.

Lilliefors, H. W. 1967. On the Kolmogorov-Smirnov test for normality with mean and variance unknown. Journal of the American Statistical Association 62(318):399-402.

Lilliefors, H. W. 1969. On the Kolmogorov-Smirnov test for the exponential distribution with mean unknown. Journal of the American Statistical Association 64(325):387-389.

Manly, B. F. J. 2004. Randomization, Bootstrap and Monte Carlo Methods in Biology. Chapman & Hall, Cornwall, Great Britain.

Parsons, F. G., and P. H. Wirsching. 1982. A Kolmogorov-Smirnov goodness-of-fit test for the two-parameter Weibull distribution when the parameters are estimated from the data. Microelectronics Reliability 22(2):163-167.

See Also

Distributions for standard cumulative distribution functions, plunif for the loguniform cumulative distribution function, and pmixnorm for the univariate normal mixture cumulative distribution function.

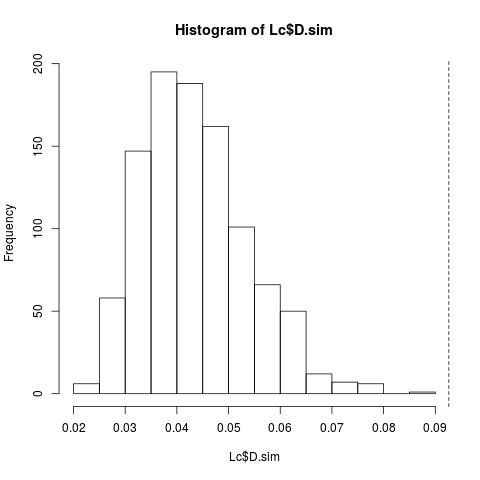
Examples

x <- runif(200)
Lc <- LcKS(x, cdf="pnorm", nreps=999)
hist(Lc$D.sim)
abline(v = Lc$D.obs, lty = 2)
print(Lc, max=50)  # Print first 50 simulated statistics
# Approximate p-value (usually) << 0.05

# Confirmation uncorrected version has increased Type II error rate when
#   using sample statistics to estimate parameters:
ks.test(x, "pnorm", mean(x), sd(x))   # p-value always larger, (usually) > 0.05

# Confirm critical values for normal distribution are correct
nreps <- 9999
x <- rnorm(25)
Lc <- LcKS(x, "pnorm", nreps=nreps)
sim.Ds <- sort(Lc$D.sim)
crit <- round(c(.8, .85, .9, .95, .99) * nreps, 0)
# Lilliefors' (1967) critical values, using improved values from
#   Parsons & Wirsching (1982) (for n=25):
# 0.141 0.148 0.157 0.172 0.201
round(sim.Ds[crit], 3)			# Approximately the same critical values

# Confirm critical values for exponential are the same as reported by Lilliefors (1969)
nreps <- 9999
x <- rexp(25)
Lc <- LcKS(x, "pexp", nreps=nreps)
sim.Ds <- sort(Lc$D.sim)
crit <- round(c(.8, .85, .9, .95, .99) * nreps, 0)
# Lilliefors' (1969) critical values (for n=25):
# 0.170 0.180 0.191 0.210 0.247
round(sim.Ds[crit], 3)			# Approximately the same critical values

## Not run: 
# Gamma and Weibull tests require functions from the 'MASS' package
# Takes time for maximum likelihood optimization of statistics
require(MASS)
x <- runif(100, min=1, max=100)
Lc <- LcKS(x, cdf="pgamma", nreps=499)
Lc$p.value

# Confirm critical values for Weibull the same as reported by Parsons & Wirsching (1982)
nreps <- 9999
x <- rweibull(25, shape=1, scale=1)
Lc <- LcKS(x, "pweibull", nreps=nreps)
sim.Ds <- sort(Lc$D.sim)
crit <- round(c(.8, .85, .9, .95, .99) * nreps, 0)
# Parsons & Wirsching (1982) critical values (for n=25):
# 0.141 0.148 0.157 0.172 0.201
round(sim.Ds[crit], 3)			# Approximately the same critical values

# Mixture test requires functions from the 'mclust' package
# Takes time to identify model parameters
require(mclust)
x <- rmixnorm(200, mean=c(10, 20), sd=2, pro=c(1,3))
Lc <- LcKS(x, cdf="pmixnorm", nreps=499, G=1:9)   # Default G (1:9) takes long time
Lc$p.value
G <- Mclust(x)$parameters$variance$G              # Optimal model has only two components
Lc <- LcKS(x, cdf="pmixnorm", nreps=499, G=G)     # Restricting to likely G saves time
# But note changes null hypothesis: now testing against just two-component mixture
Lc$p.value

## End(Not run)

Results

R version 3.3.1 (2016-06-21) -- "Bug in Your Hair"
Copyright (C) 2016 The R Foundation for Statistical Computing
Platform: x86_64-pc-linux-gnu (64-bit)

R is free software and comes with ABSOLUTELY NO WARRANTY.
You are welcome to redistribute it under certain conditions.
Type 'license()' or 'licence()' for distribution details.

R is a collaborative project with many contributors.
Type 'contributors()' for more information and
'citation()' on how to cite R or R packages in publications.

Type 'demo()' for some demos, 'help()' for on-line help, or
'help.start()' for an HTML browser interface to help.
Type 'q()' to quit R.

> library(KScorrect)
> png(filename="/home/ddbj/snapshot/RGM3/R_CC/result/KScorrect/LcKS.Rd_%03d_medium.png", width=480, height=480)
> ### Name: LcKS
> ### Title: Lilliefors-corrected Kolmogorov-Smirnoff Goodness-Of-Fit Test
> ### Aliases: LcKS
> 
> ### ** Examples
> 
> x <- runif(200)
> Lc <- LcKS(x, cdf="pnorm", nreps=999)
> hist(Lc$D.sim)
> abline(v = Lc$D.obs, lty = 2)
> print(Lc, max=50)  # Print first 50 simulated statistics
$D.obs
[1] 0.09262385

$D.sim
 [1] 0.03706487 0.03842167 0.02583074 0.04725934 0.04539004 0.02914926
 [7] 0.04583008 0.04229889 0.04126987 0.03473239 0.03666469 0.05564759
[13] 0.04883253 0.03809087 0.03073768 0.05027152 0.04581409 0.03636533
[19] 0.03939353 0.02878655 0.05871600 0.03299456 0.07644536 0.05299444
[25] 0.02932849 0.04356083 0.05483117 0.03369578 0.03039681 0.06930097
[31] 0.04429688 0.03832761 0.06029079 0.06807311 0.04295805 0.06358311
[37] 0.05347978 0.03548766 0.02621571 0.03770416 0.03833268 0.04038596
[43] 0.06787367 0.03784615 0.03743014 0.04957043 0.04784248 0.03803586
[49] 0.05131795 0.05864168
 [ reached getOption("max.print") -- omitted 949 entries ]

$p.value
[1] 0.001

> # Approximate p-value (usually) << 0.05
> 
> # Confirmation uncorrected version has increased Type II error rate when
> #   using sample statistics to estimate parameters:
> ks.test(x, "pnorm", mean(x), sd(x))   # p-value always larger, (usually) > 0.05

	One-sample Kolmogorov-Smirnov test

data:  x
D = 0.092624, p-value = 0.06466
alternative hypothesis: two-sided

> 
> # Confirm critical values for normal distribution are correct
> nreps <- 9999
> x <- rnorm(25)
> Lc <- LcKS(x, "pnorm", nreps=nreps)
> sim.Ds <- sort(Lc$D.sim)
> crit <- round(c(.8, .85, .9, .95, .99) * nreps, 0)
> # Lilliefors' (1967) critical values, using improved values from
> #   Parsons & Wirsching (1982) (for n=25):
> # 0.141 0.148 0.157 0.172 0.201
> round(sim.Ds[crit], 3)			# Approximately the same critical values
[1] 0.142 0.150 0.159 0.173 0.203
> 
> # Confirm critical values for exponential are the same as reported by Lilliefors (1969)
> nreps <- 9999
> x <- rexp(25)
> Lc <- LcKS(x, "pexp", nreps=nreps)
> sim.Ds <- sort(Lc$D.sim)
> crit <- round(c(.8, .85, .9, .95, .99) * nreps, 0)
> # Lilliefors' (1969) critical values (for n=25):
> # 0.170 0.180 0.191 0.210 0.247
> round(sim.Ds[crit], 3)			# Approximately the same critical values
[1] 0.170 0.179 0.191 0.211 0.251
> 
> ## Not run: 
> ##D # Gamma and Weibull tests require functions from the 'MASS' package
> ##D # Takes time for maximum likelihood optimization of statistics
> ##D require(MASS)
> ##D x <- runif(100, min=1, max=100)
> ##D Lc <- LcKS(x, cdf="pgamma", nreps=499)
> ##D Lc$p.value
> ##D 
> ##D # Confirm critical values for Weibull the same as reported by Parsons & Wirsching (1982)
> ##D nreps <- 9999
> ##D x <- rweibull(25, shape=1, scale=1)
> ##D Lc <- LcKS(x, "pweibull", nreps=nreps)
> ##D sim.Ds <- sort(Lc$D.sim)
> ##D crit <- round(c(.8, .85, .9, .95, .99) * nreps, 0)
> ##D # Parsons & Wirsching (1982) critical values (for n=25):
> ##D # 0.141 0.148 0.157 0.172 0.201
> ##D round(sim.Ds[crit], 3)			# Approximately the same critical values
> ##D 
> ##D # Mixture test requires functions from the 'mclust' package
> ##D # Takes time to identify model parameters
> ##D require(mclust)
> ##D x <- rmixnorm(200, mean=c(10, 20), sd=2, pro=c(1,3))
> ##D Lc <- LcKS(x, cdf="pmixnorm", nreps=499, G=1:9)   # Default G (1:9) takes long time
> ##D Lc$p.value
> ##D G <- Mclust(x)$parameters$variance$G              # Optimal model has only two components
> ##D Lc <- LcKS(x, cdf="pmixnorm", nreps=499, G=G)     # Restricting to likely G saves time
> ##D # But note changes null hypothesis: now testing against just two-component mixture
> ##D Lc$p.value
> ## End(Not run)
> 
> 
> 
> 
> 
> 
> dev.off()
null device 
          1 
>