ISS solver for linear model with lasso penalty

Description

Solver for the entire solution path of coefficients for ISS.

Usage

iss(X, y, intercept = TRUE, normalize = TRUE, nvar = min(dim(X)))

Arguments

Details

The ISS solver computes the whole regularization path for lasso-penalty for linear model. It gives the piecewise constant solution path for Bregman Inverse Scale Space Differential Inclusion. It is the asymptotic limit of LB method with kaapa goes to infinity and alpha goes to zero.

Value

An "LB" class object is returned. The list contains the call, the family, the path, the intercept term a0 and value for alpha, kappa, iter, and meanvalue, scale factor of X, meanx and normx.

Author(s)

Feng Ruan, Jiechao Xiong and Yuan Yao

References

Ohser, Ruan, Xiong, Yao and Yin, Sparse Recovery via Differential Inclusions, http://arxiv.org/abs/1406.7728

Examples

#Examples in the reference paper
library(MASS)
library(lars)
library(MASS)
library(lars)
n = 80;p = 100;k = 30;sigma = 1
Sigma = 1/(3*p)*matrix(rep(1,p^2),p,p)
diag(Sigma) = 1
A = mvrnorm(n, rep(0, p), Sigma)
u_ref = rep(0,p)
supp_ref = 1:k
u_ref[supp_ref] = rnorm(k)
u_ref[supp_ref] = u_ref[supp_ref]+sign(u_ref[supp_ref])
b = as.vector(A%*%u_ref + sigma*rnorm(n))
lasso = lars(A,b,normalize=FALSE,intercept=FALSE,max.steps=100)
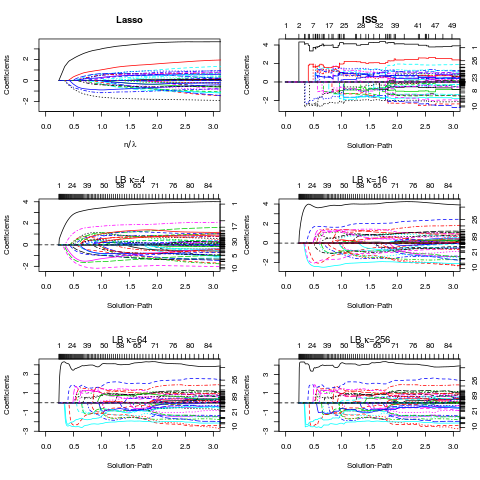
par(mfrow=c(3,2))
matplot(n/lasso$lambda, lasso$beta[1:100,], xlab = bquote(n/lambda), 
        ylab = "Coefficients", xlim=c(0,3),ylim=c(range(lasso$beta)),type='l', main="Lasso")
object = iss(A,b,intercept=FALSE,normalize=FALSE)
plot(object,xlim=c(0,3),main=bquote("ISS"))
kappa_list = c(4,16,64,256)
alpha_list = 1/10/kappa_list
for (i in 1:4){
  object <- lb(A,b,kappa_list[i],alpha_list[i],family="gaussian",group=FALSE,
               trate=20,intercept=FALSE,normalize=FALSE)
  plot(object,xlim=c(0,3),main=bquote(paste("LB ",kappa,"=",.(kappa_list[i]))))
}

Results

R version 3.3.1 (2016-06-21) -- "Bug in Your Hair"
Copyright (C) 2016 The R Foundation for Statistical Computing
Platform: x86_64-pc-linux-gnu (64-bit)

R is free software and comes with ABSOLUTELY NO WARRANTY.
You are welcome to redistribute it under certain conditions.
Type 'license()' or 'licence()' for distribution details.

R is a collaborative project with many contributors.
Type 'contributors()' for more information and
'citation()' on how to cite R or R packages in publications.

Type 'demo()' for some demos, 'help()' for on-line help, or
'help.start()' for an HTML browser interface to help.
Type 'q()' to quit R.

> library(Libra)
Loading required package: nnls
Loaded Libra 1.5

> png(filename="/home/ddbj/snapshot/RGM3/R_CC/result/Libra/iss.Rd_%03d_medium.png", width=480, height=480)
> ### Name: iss
> ### Title: ISS solver for linear model with lasso penalty
> ### Aliases: iss
> ### Keywords: regression
> 
> ### ** Examples
> 
> #Examples in the reference paper
> library(MASS)
> library(lars)
Loaded lars 1.2

> library(MASS)
> library(lars)
> n = 80;p = 100;k = 30;sigma = 1
> Sigma = 1/(3*p)*matrix(rep(1,p^2),p,p)
> diag(Sigma) = 1
> A = mvrnorm(n, rep(0, p), Sigma)
> u_ref = rep(0,p)
> supp_ref = 1:k
> u_ref[supp_ref] = rnorm(k)
> u_ref[supp_ref] = u_ref[supp_ref]+sign(u_ref[supp_ref])
> b = as.vector(A%*%u_ref + sigma*rnorm(n))
> lasso = lars(A,b,normalize=FALSE,intercept=FALSE,max.steps=100)
> par(mfrow=c(3,2))
> matplot(n/lasso$lambda, lasso$beta[1:100,], xlab = bquote(n/lambda), 
+         ylab = "Coefficients", xlim=c(0,3),ylim=c(range(lasso$beta)),type='l', main="Lasso")
> object = iss(A,b,intercept=FALSE,normalize=FALSE)
> plot(object,xlim=c(0,3),main=bquote("ISS"))
> kappa_list = c(4,16,64,256)
> alpha_list = 1/10/kappa_list
> for (i in 1:4){
+   object <- lb(A,b,kappa_list[i],alpha_list[i],family="gaussian",group=FALSE,
+                trate=20,intercept=FALSE,normalize=FALSE)
+   plot(object,xlim=c(0,3),main=bquote(paste("LB ",kappa,"=",.(kappa_list[i]))))
+ }
> 
> 
> 
> 
> 
> 
> dev.off()
null device 
          1 
>