Last data update: 2014.03.03

 R: Simulation of 1-Dim Stochastic Differential Equation
snssde1dR Documentation

Simulation of 1-Dim Stochastic Differential Equation

Description

The (S3) generic function snssde1d of simulation of solutions to 1-dim stochastic differential equations of Ito or Stratonovich type, with different methods.

Usage

snssde1d(N, ...)
## Default S3 method:
snssde1d(N = 1000, M = 1, x0 = 0, t0 = 0, T = 1, Dt, 
   drift, diffusion, alpha = 0.5, mu = 0.5, type = c("ito", "str"), 
   method = c("euler", "milstein", "predcorr", "smilstein", "taylor", 
   "heun", "rk1", "rk2", "rk3"), ...)
						   
						   
## S3 method for class 'snssde1d'
summary(object, ...)
## S3 method for class 'snssde1d'
time(x, ...)
## S3 method for class 'snssde1d'
mean(x, ...)
## S3 method for class 'snssde1d'
median(x, ...)
## S3 method for class 'snssde1d'
quantile(x, ...)
## S3 method for class 'snssde1d'
kurtosis(x, ...)
## S3 method for class 'snssde1d'
skewness(x, ...)
## S3 method for class 'snssde1d'
moment(x, order = 2, ...)
## S3 method for class 'snssde1d'
bconfint(x, level=0.95, ...)
## S3 method for class 'snssde1d'
plot(x, ...)
## S3 method for class 'snssde1d'
lines(x, ...)
## S3 method for class 'snssde1d'
points(x, ...)

Arguments

N

number of simulation steps.

M

number of trajectories.

x0

initial value of the process at time t0.

t0

initial time.

T

final time.

Dt

time step of the simulation (discretization). If it is missing a default Dt = (T-t0)/N.

drift

drift coefficient: an expression of two variables t and x.

diffusion

diffusion coefficient: an expression of two variables t and x.

alpha, mu

weight of the predictor-corrector scheme; the default alpha = 0.5 and mu = 0.5.

type

if type="ito" simulation sde of Ito type, else type="str" simulation sde of Stratonovich type; the default type="ito".

method

numerical methods of simulation, the default method = "euler".

x, object

an object inheriting from class "snssde1d".

order

order of moment.

level

the confidence level required.

...

further arguments for (non-default) methods.

Details

The function snssde1d returns a ts x of length N+1; i.e. solution of the sde of Ito or Stratonovich types; If Dt is not specified, then the best discretization Dt = (T-t0)/N.

The Ito stochastic differential equation is:

dX(t) = a(t,X(t))*dt + b(t,X(t))*dW(t)

Stratonovich sde :

dX(t) = a(t,X(t))*dt + b(t,X(t)) o dW(t)

The methods of approximation are classified according to their different properties. Mainly two criteria of optimality are used in the literature: the strong and the weak (orders of) convergence. The method of simulation can be one among: Euler-Maruyama Order 0.5, Milstein Order 1, Milstein Second-Order, Predictor-Corrector method, Ito-Taylor Order 1.5, Heun Order 2 and Runge-Kutta Order 1, 2 and 3.

For more details see vignette("SDEs").

Value

snssde1d returns an object inheriting from class "snssde1d".

X

an invisible ts object.

drift

drift coefficient.

diffusion

diffusion coefficient.

type

type of sde.

method

the numerical method used.

Author(s)

A.C. Guidoum, K. Boukhetala.

References

Friedman, A. (1975). Stochastic differential equations and applications. Volume 1, ACADEMIC PRESS.

Henderson, D. and Plaschko,P. (2006). Stochastic differential equations in science and engineering. World Scientific.

Allen, E. (2007). Modeling with Ito stochastic differential equations. Springer-Verlag.

Jedrzejewski, F. (2009). Modeles aleatoires et physique probabiliste. Springer-Verlag.

Iacus, S.M. (2008). Simulation and inference for stochastic differential equations: with R examples. Springer-Verlag, New York.

Kloeden, P.E, and Platen, E. (1989). A survey of numerical methods for stochastic differential equations. Stochastic Hydrology and Hydraulics, 3, 155–178.

Kloeden, P.E, and Platen, E. (1991a). Relations between multiple ito and stratonovich integrals. Stochastic Analysis and Applications, 9(3), 311–321.

Kloeden, P.E, and Platen, E. (1991b). Stratonovich and ito stochastic taylor expansions. Mathematische Nachrichten, 151, 33–50.

Kloeden, P.E, and Platen, E. (1995). Numerical Solution of Stochastic Differential Equations. Springer-Verlag, New York.

Oksendal, B. (2000). Stochastic Differential Equations: An Introduction with Applications. 5th edn. Springer-Verlag, Berlin.

Platen, E. (1980). Weak convergence of approximations of ito integral equations. Z Angew Math Mech. 60, 609–614.

Platen, E. and Bruti-Liberati, N. (2010). Numerical Solution of Stochastic Differential Equations with Jumps in Finance. Springer-Verlag, New York

Saito, Y, and Mitsui, T. (1993). Simulation of Stochastic Differential Equations. The Annals of the Institute of Statistical Mathematics, 3, 419–432.

See Also

snssde2d and snssde3d for 2 and 3-dim sde.

sde.sim in package sde.

simulate in package "yuima".

Examples


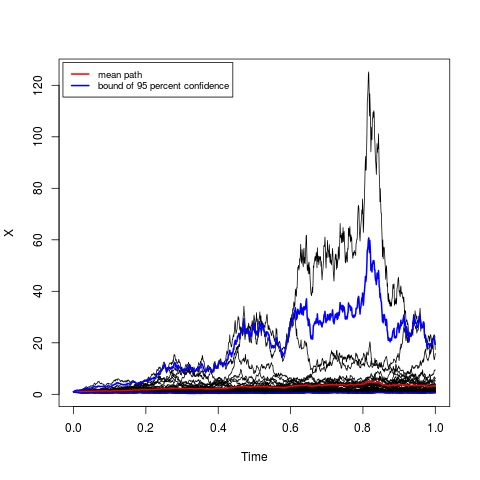
## Example 1: Ito sde
## dX(t) = 2*(3-X(t)) dt + 2*X(t) dW(t)
set.seed(1234)

f <- expression(2*(3-x) )
g <- expression(2*x)
res <- snssde1d(drift=f,diffusion=g,M=50,x0=1,N=1000)
res
## Sim <- res$X
summary(res)
plot(res,plot.type="single")
lines(time(res),mean(res),col=2,lwd=2)
lines(time(res),bconfint(res,level=0.95)[,1],col=4,lwd=2)
lines(time(res),bconfint(res,level=0.95)[,2],col=4,lwd=2)
legend("topleft",c("mean path",paste("bound of", 95,"percent confidence")),
       inset = .01,col=c(2,4),lwd=2,cex=0.8)

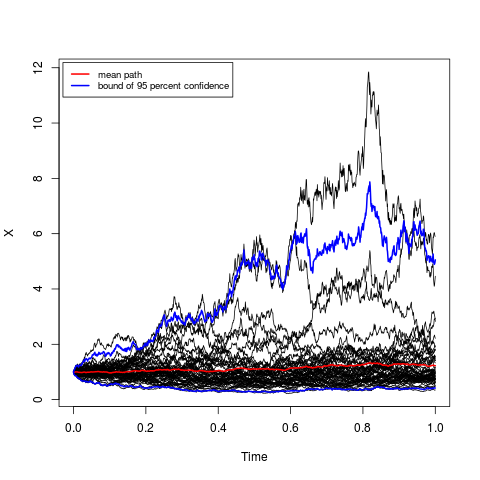
## Example 2: Stratonovich sde
## dX(t) = ((2-X(t))/(2-t)) dt + X(t) o dW(t)
set.seed(1234)

f <- expression((2-x)/(2-t))
g <- expression(x)
res1 <- snssde1d(type="str",drift=f,diffusion=g,M=50,x0=1,N=1000,
                 method="milstein")
res1
summary(res1)
plot(res1,plot.type="single")
lines(time(res1),mean(res1),col=2,lwd=2)
lines(time(res1),bconfint(res1,level=0.95)[,1],col=4,lwd=2)
lines(time(res1),bconfint(res1,level=0.95)[,2],col=4,lwd=2)
legend("topleft",c("mean path",paste("bound of", 95,"percent confidence")),
       inset = .01,col=c(2,4),lwd=2,cex=0.8)

Results


R version 3.3.1 (2016-06-21) -- "Bug in Your Hair"
Copyright (C) 2016 The R Foundation for Statistical Computing
Platform: x86_64-pc-linux-gnu (64-bit)

R is free software and comes with ABSOLUTELY NO WARRANTY.
You are welcome to redistribute it under certain conditions.
Type 'license()' or 'licence()' for distribution details.

R is a collaborative project with many contributors.
Type 'contributors()' for more information and
'citation()' on how to cite R or R packages in publications.

Type 'demo()' for some demos, 'help()' for on-line help, or
'help.start()' for an HTML browser interface to help.
Type 'q()' to quit R.

> library(Sim.DiffProc)
Package 'Sim.DiffProc' version 3.2 loaded.
help(Sim.DiffProc) for summary information.
> png(filename="/home/ddbj/snapshot/RGM3/R_CC/result/Sim.DiffProc/snssde1d.Rd_%03d_medium.png", width=480, height=480)
> ### Name: snssde1d
> ### Title: Simulation of 1-Dim Stochastic Differential Equation
> ### Aliases: snssde1d snssde1d.default summary.snssde1d print.snssde1d
> ###   time.snssde1d mean.snssde1d median.snssde1d quantile.snssde1d
> ###   kurtosis.snssde1d skewness.snssde1d moment.snssde1d bconfint.snssde1d
> ###   plot.snssde1d points.snssde1d lines.snssde1d
> ### Keywords: sde ts mts
> 
> ### ** Examples
> 
> 
> ## Example 1: Ito sde
> ## dX(t) = 2*(3-X(t)) dt + 2*X(t) dW(t)
> set.seed(1234)
> 
> f <- expression(2*(3-x) )
> g <- expression(2*x)
> res <- snssde1d(drift=f,diffusion=g,M=50,x0=1,N=1000)
> res
Ito Sde 1D:
	| dX(t) = 2 * (3 - X(t)) * dt + 2 * X(t) * dW(t)
Method:
	| Euler scheme of order 0.5
Summary:
	| Size of process	| N  = 1000.
	| Number of simulation	| M  = 50.
	| Initial value		| x0 = 1.
	| Time of process	| t in [0,1].
	| Discretization	| Dt = 0.001.
> ## Sim <- res$X
> summary(res)

	Monte-Carlo Statistics for X(t) at final time T = 1

                                X
Mean                     3.142025
Variance                18.561062
Median                   1.715538
First quartile           1.083597
Third quartile           2.815213
Skewness                 2.992461
Kurtosis                11.728186
Moment of order 2       18.189840
Moment of order 3      239.294490
Moment of order 4     4040.512782
Moment of order 5    69072.177096
Bound conf Inf (95%)     0.654362
Bound conf Sup (95%)    17.057492
> plot(res,plot.type="single")
> lines(time(res),mean(res),col=2,lwd=2)
> lines(time(res),bconfint(res,level=0.95)[,1],col=4,lwd=2)
> lines(time(res),bconfint(res,level=0.95)[,2],col=4,lwd=2)
> legend("topleft",c("mean path",paste("bound of", 95,"percent confidence")),
+        inset = .01,col=c(2,4),lwd=2,cex=0.8)
> 
> ## Example 2: Stratonovich sde
> ## dX(t) = ((2-X(t))/(2-t)) dt + X(t) o dW(t)
> set.seed(1234)
> 
> f <- expression((2-x)/(2-t))
> g <- expression(x)
> res1 <- snssde1d(type="str",drift=f,diffusion=g,M=50,x0=1,N=1000,
+                  method="milstein")
> res1
Stratonovich Sde 1D:
	| dX(t) = (2 - X(t))/(2 - t) * dt + X(t) o dW(t)
Method:
	| Milstein scheme of order 1
Summary:
	| Size of process	| N  = 1000.
	| Number of simulation	| M  = 50.
	| Initial value		| x0 = 1.
	| Time of process	| t in [0,1].
	| Discretization	| Dt = 0.001.
> summary(res1)

	Monte-Carlo Statistics for X(t) at final time T = 1

                             X
Mean                  1.226419
Variance              0.995357
Median                0.875143
First quartile        0.734474
Third quartile        1.385116
Skewness              2.876349
Kurtosis             12.297469
Moment of order 2     0.975450
Moment of order 3     2.856342
Moment of order 4    12.183552
Moment of order 5    52.537073
Bound conf Inf (95%)  0.477809
Bound conf Sup (95%)  4.115370
> plot(res1,plot.type="single")
> lines(time(res1),mean(res1),col=2,lwd=2)
> lines(time(res1),bconfint(res1,level=0.95)[,1],col=4,lwd=2)
> lines(time(res1),bconfint(res1,level=0.95)[,2],col=4,lwd=2)
> legend("topleft",c("mean path",paste("bound of", 95,"percent confidence")),
+        inset = .01,col=c(2,4),lwd=2,cex=0.8)
> 
> 
> 
> 
> 
> dev.off()
null device 
          1 
>


Created & Maintained by Osamu Ogasawara (osamu.ogasawara@gmail.com) and IMSBIO